小数と分数が混じった式の解き方 大人のやり直し算数の第一歩 計算方法の解説 無料
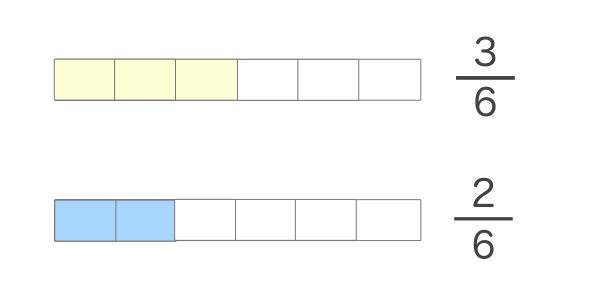
これを 分数の通分 といいます。 基本的には、 それぞれの分母にある数の最小公倍数で揃えていきます。 それでは、分数の通分について手順を追ってみていきましょう。 を計算しま分数とは、ある数を 0 でない他の数で割った商を、横線の上（分子）に割られる数、横線の下（分母）に割る数を記して表したものです。 このページでは、分数の計算のやり方をまとめています。
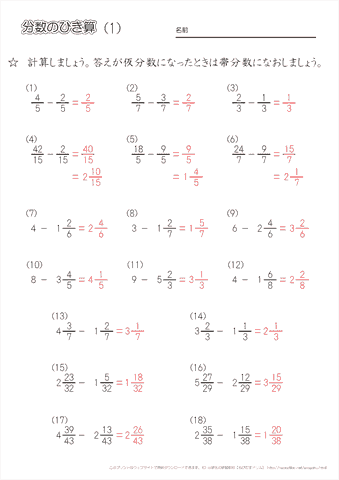
分数の引き算の解き方
分数の引き算の解き方-電卓の使い方 引き算をおこなう2つの分数の分母・分子を電卓に入力して「計算」ボタンを押してください。 少数を含んだ分数の引き算にも対応しています。 少数の分数の場合、整数の分数に変「ルートがある分数の足し算引き算って、どうやって計算するの？」ルートがある分数の計算方法は次のとおり。ルートの分数計算・足し算引き算4ステップ1 平方根 解き方
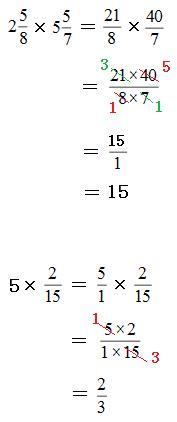
分数の計算方法を解説 分数は小数よりもずっとサボれる
平方根の足し算、引き算のやり方 平方根の足し算、引き算は注意です！！ 掛け算のときには、ルートの中身を掛ければOKでした。 $$\sqrt{2}\times \sqrt{3}=\sqrt{6}$$ ⇒ 平方根 中学1年の数学で学習する「方程式」 今回は「 分数をふくむ方程式 」の解き方がよくわからないという中学生に向けて、詳しく解説しています。 ・この記事では、次の3つの内容を詳しこんにちは、ウチダです。 今日は、小学校高学年で習う関門 「分数」 について、考え方と計算のやり方(足し算引き算掛け算割り算)を詳しく解説していきます！ 分数とは比である おっと、いきなり
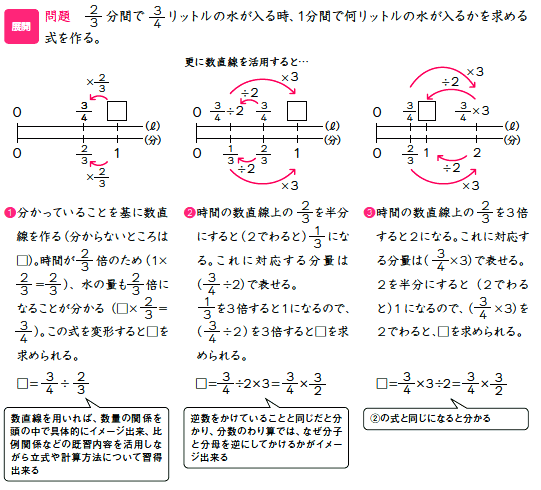
分数式の足し算と引き算（分母が同じ場合） 分母が同じである 分数式の足し算 は， 分母はそのままで分子は足し算 です： 例 \dfrac {2x} {x^21}\dfrac {3} {x^21}=\dfrac {2x3} 次のような分数の場合は 答えはどのようになるのでしょうか？ 頑張って チャレンジしてみて下さい。 どうだったでしょうか？ それでは 解き方を見ていきます。 考え方は 今までと同 グラフの書き方、分数不等式、微分積分を解説 22年3月16日 この記事では、「分数関数」についてわかりやすく解説していきます。 分数関数のグラフの書き方や不等式の解き方、
分数の引き算の解き方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 1 |  1 |  1 |
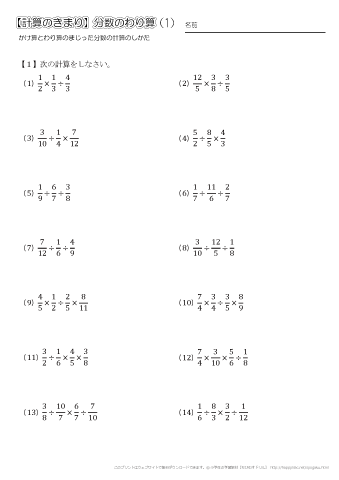 1 |  1 | 1 |
 1 | 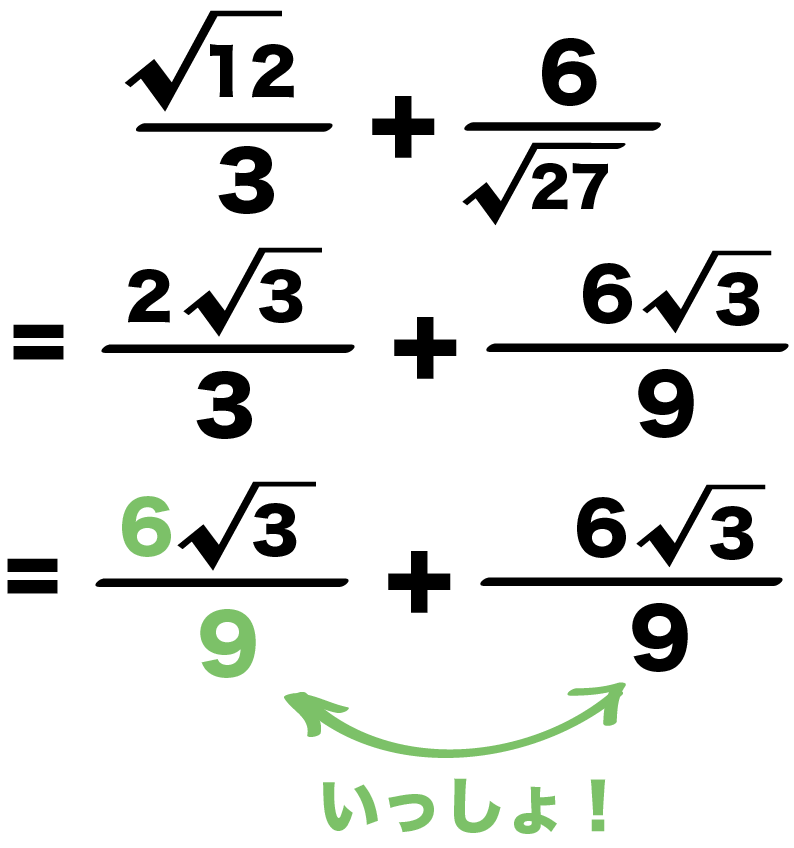 1 |  1 |
 1 |  1 |  1 |
 1 | 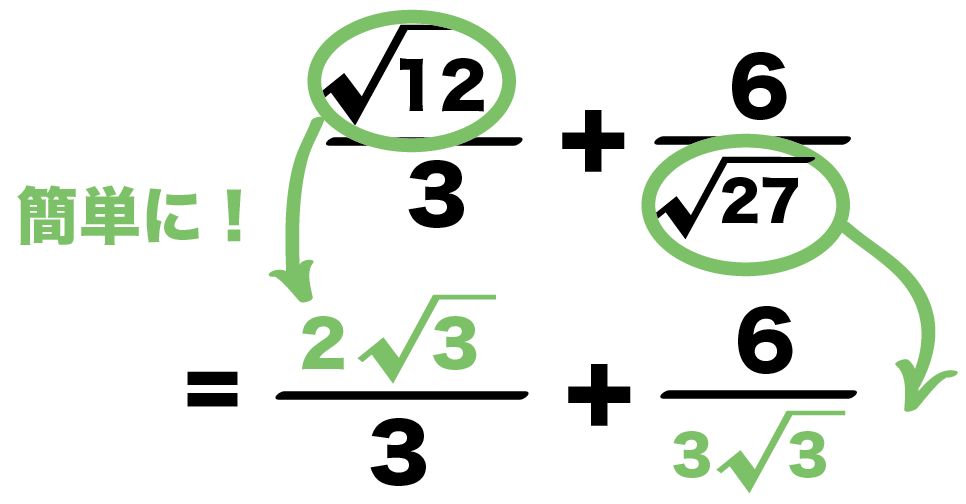 1 |  1 |
 1 |  1 |  1 |
 1 |  1 |  1 |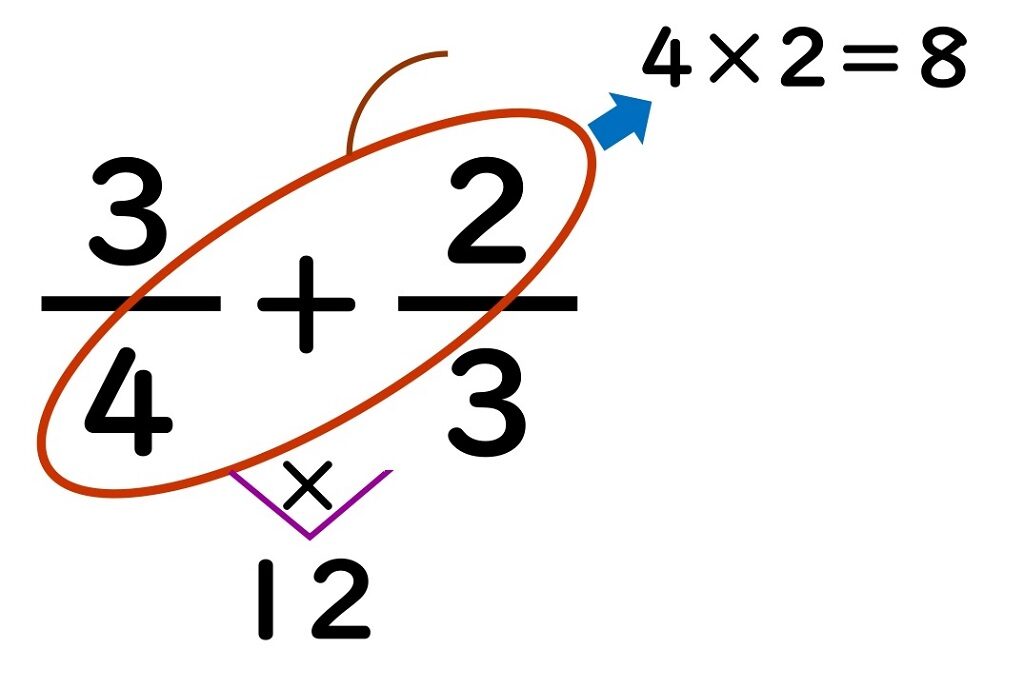
 1 |  1 | 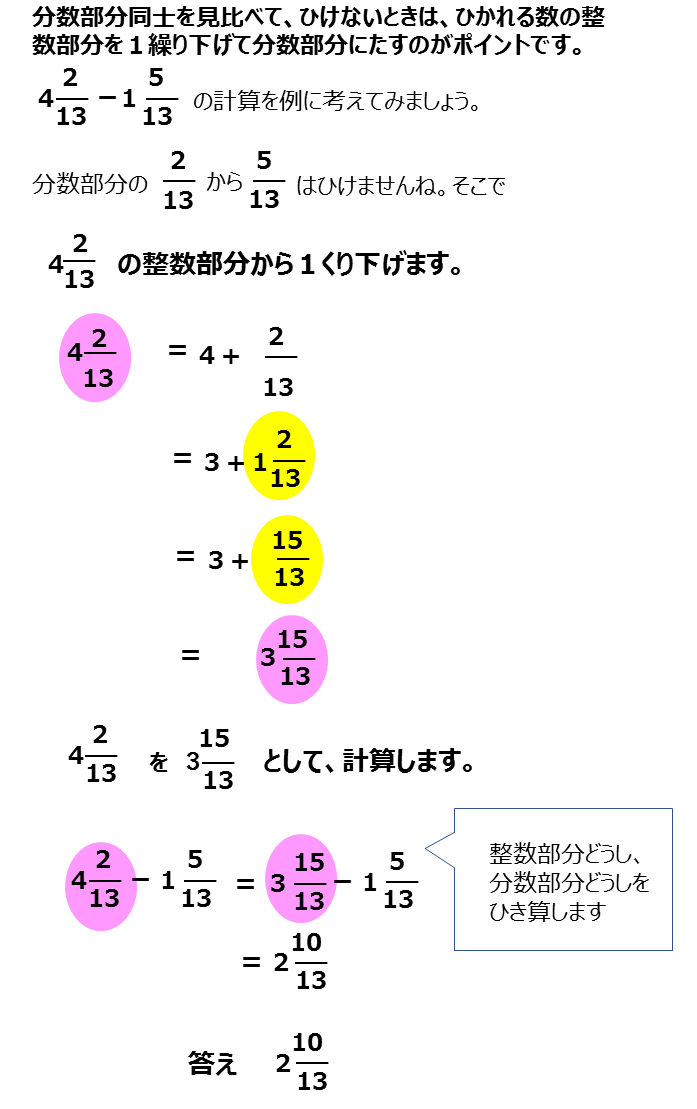 1 |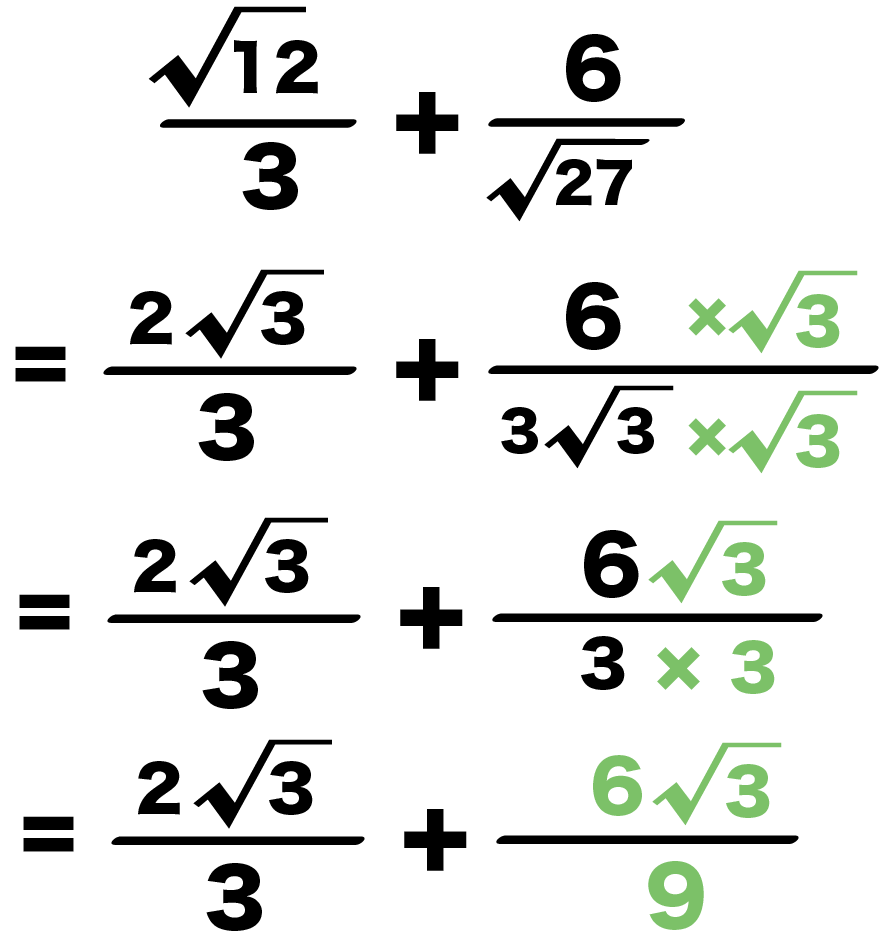
 1 |  1 | 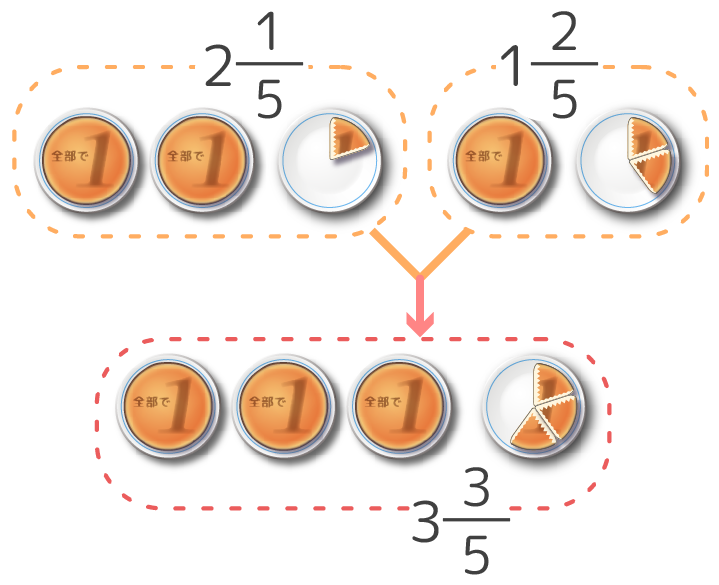 1 |
 1 |  1 | 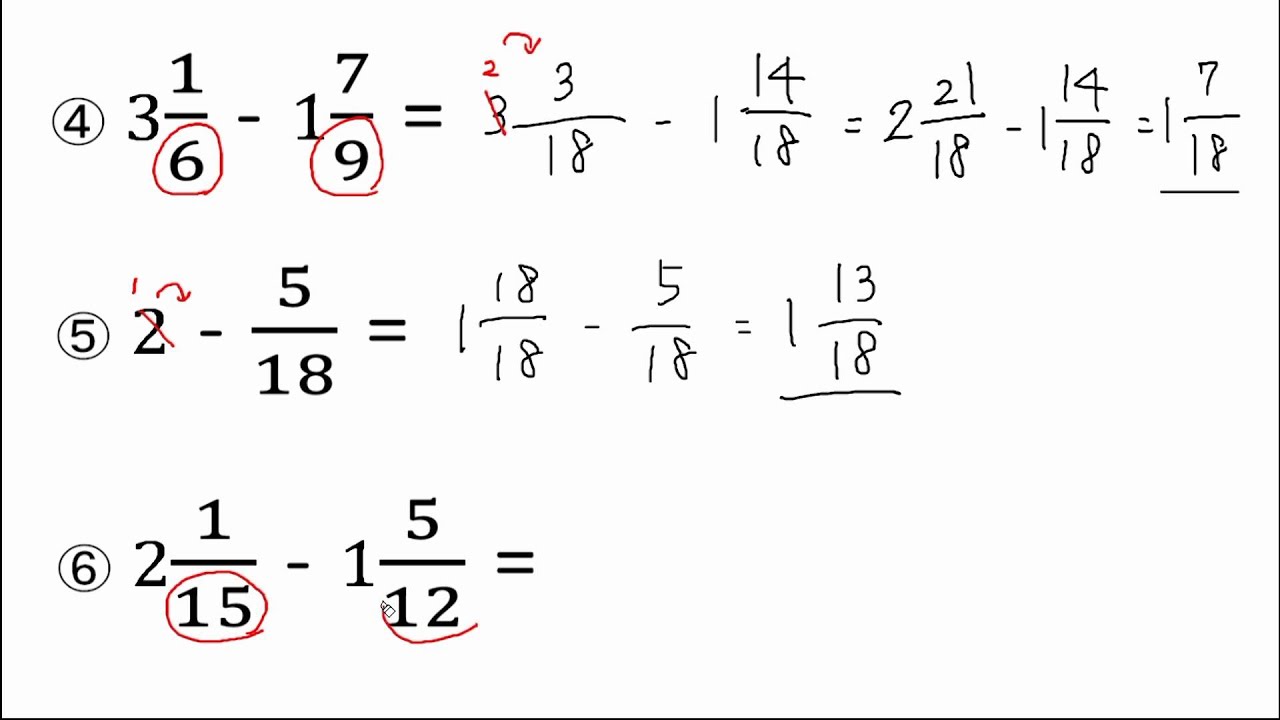 1 |
1 |  1 |  1 |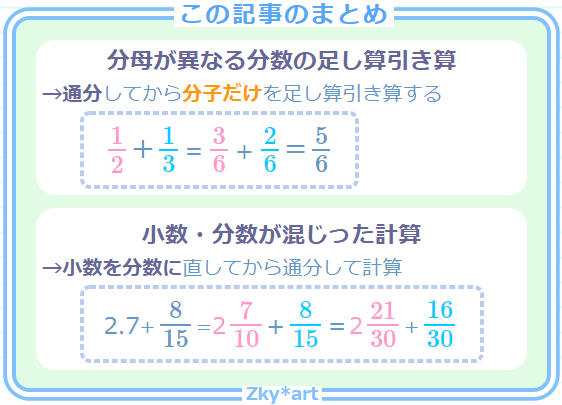
1 | 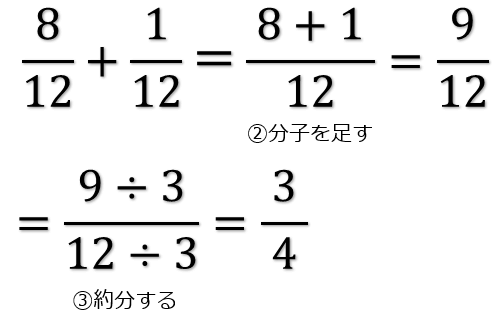 1 |  1 |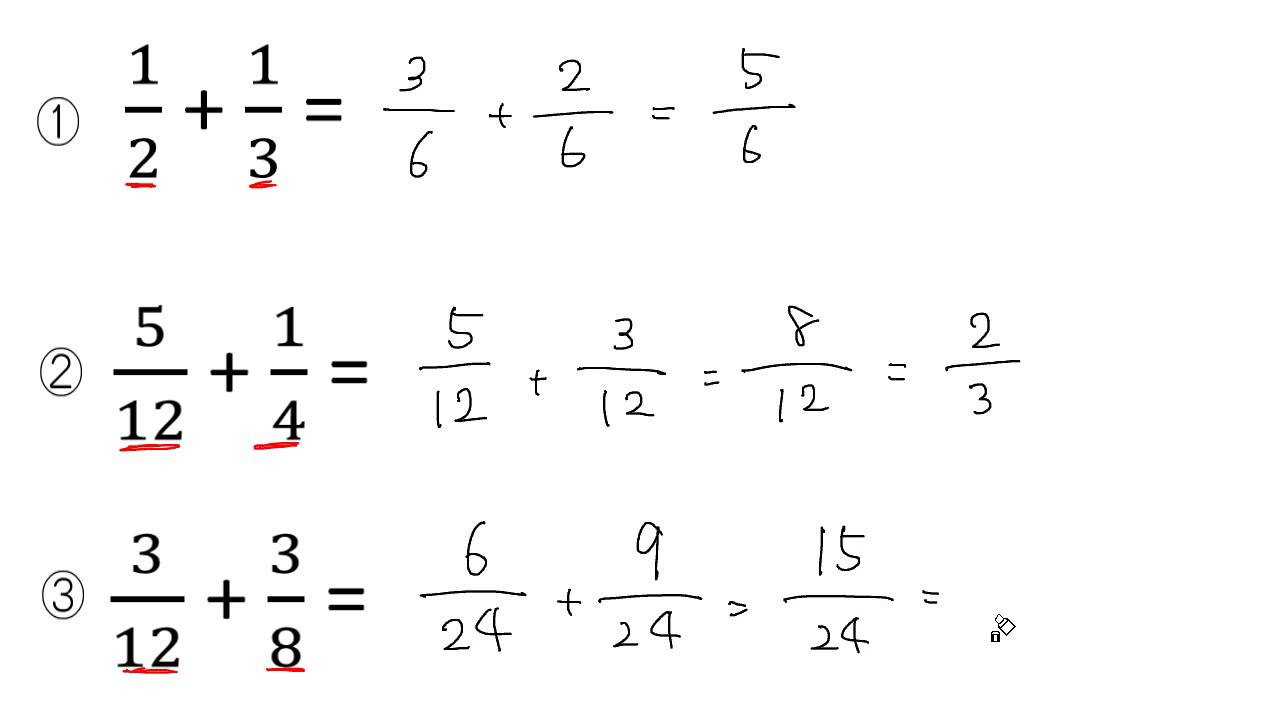
 1 | 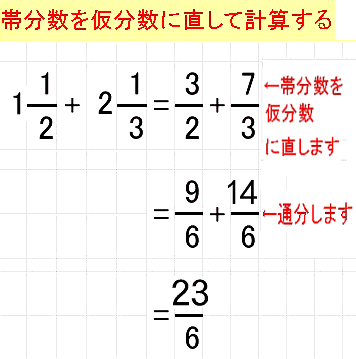 1 |  1 |
 1 |  1 | 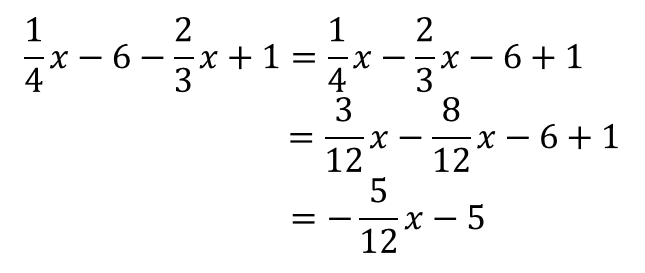 1 |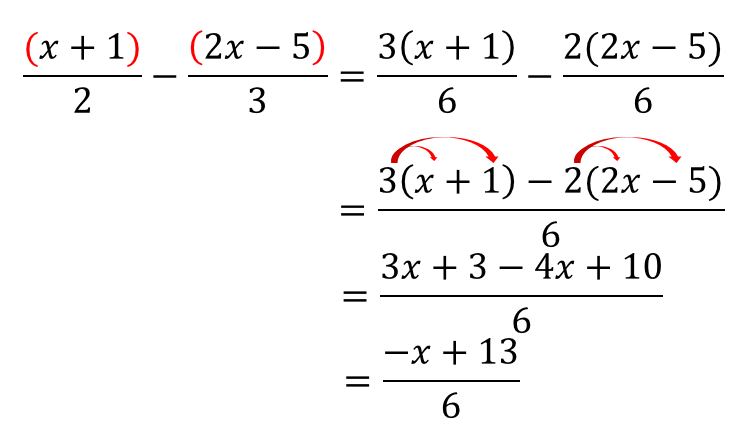
1 | 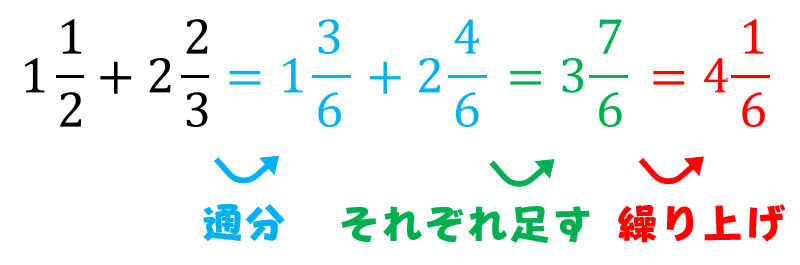 1 |  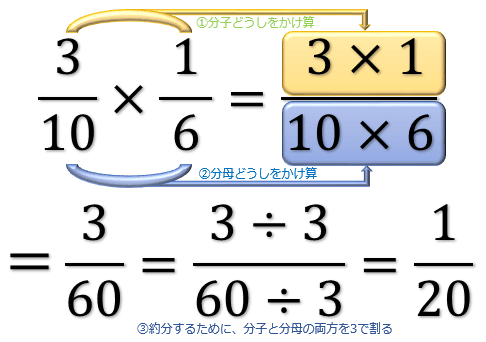1 |
 1 |  1 | 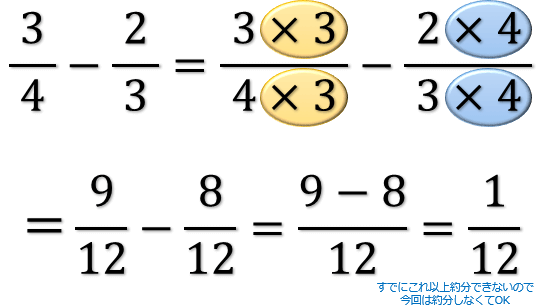 1 |
 1 | 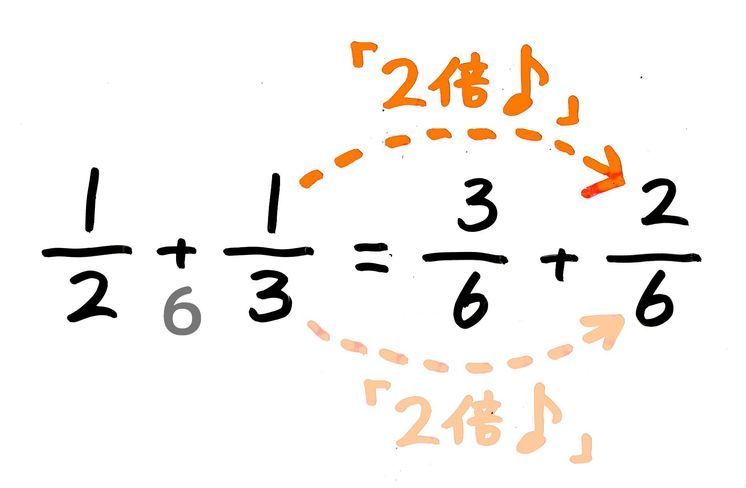 1 |  1 |
 1 | 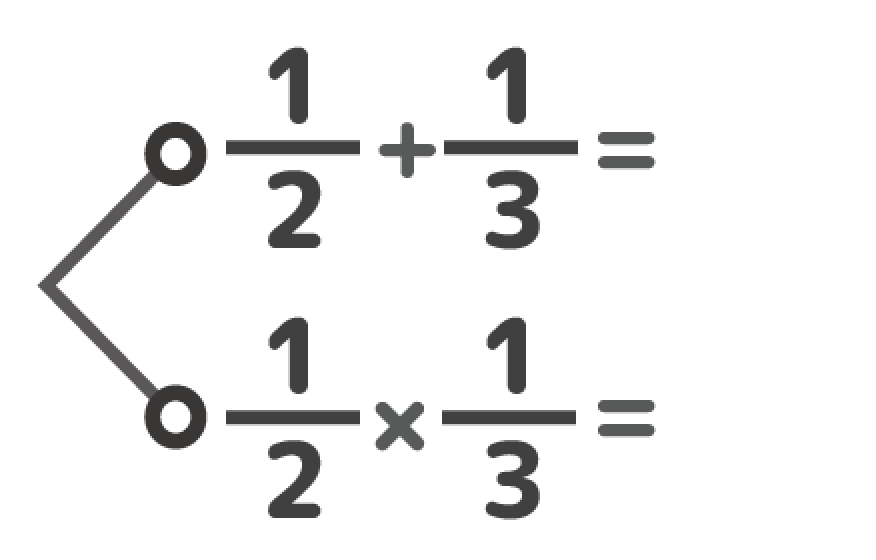 1 |  1 |
 1 | 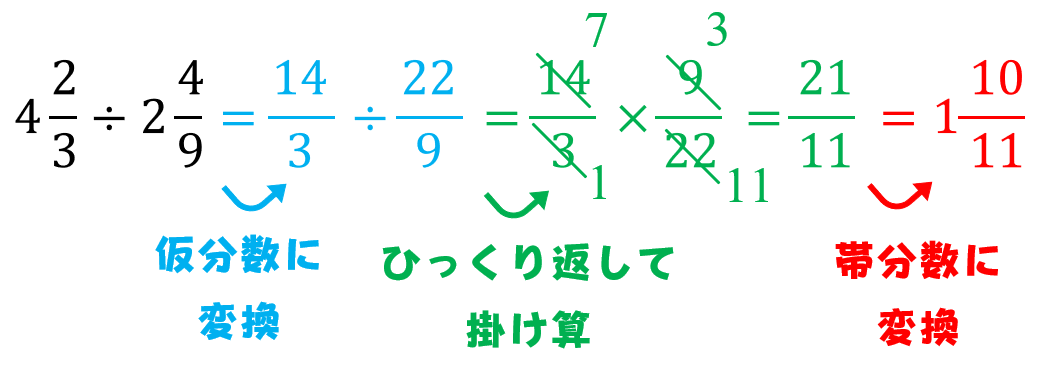 1 |  1 |
 1 | 1 |  1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 | 1 |  1 |
 1 | 1 | 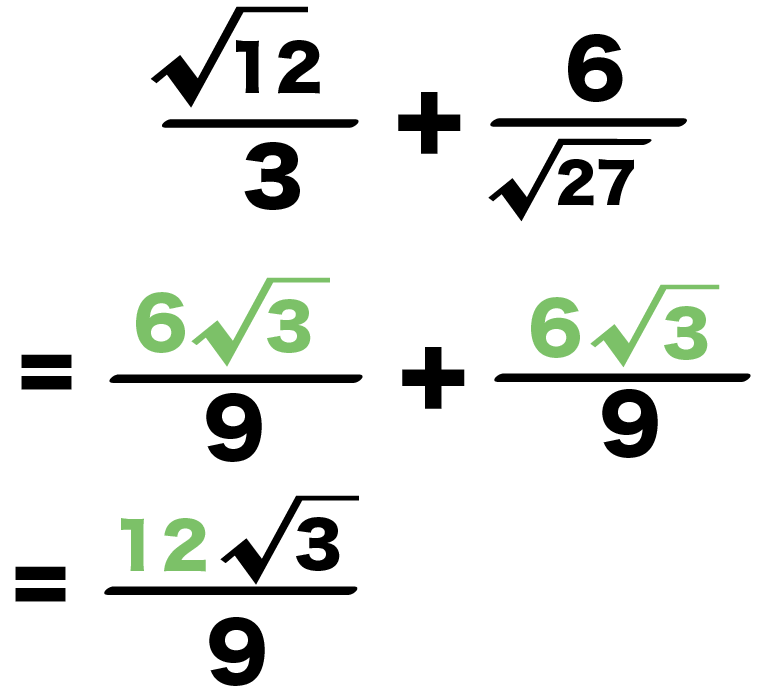 1 |
1 |  1 |  1 |
 1 | 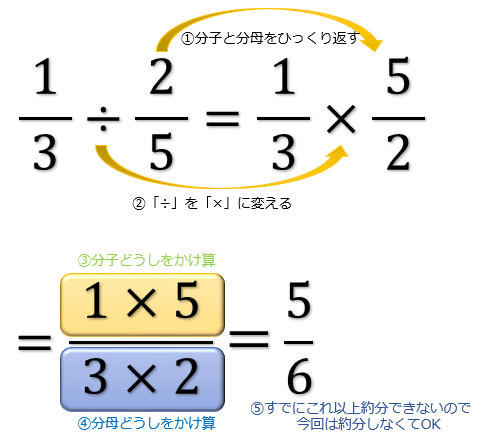 1 | 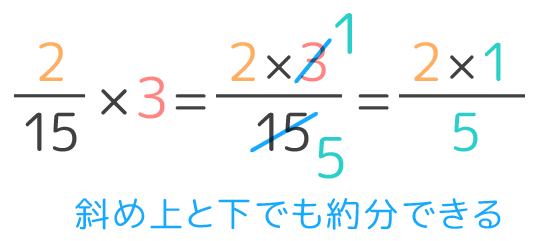 1 |
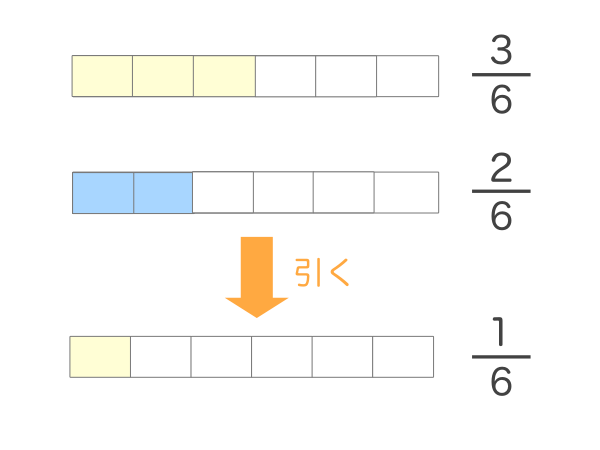 1 | 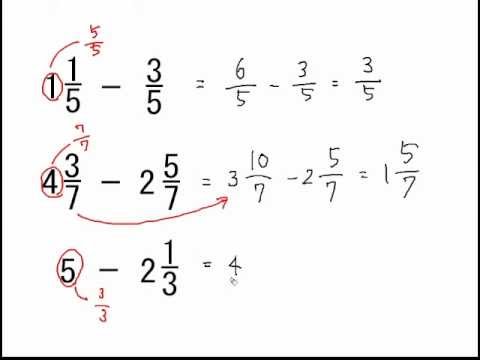 1 | 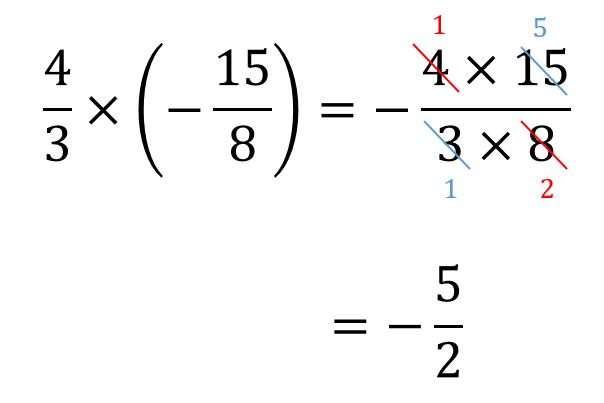 1 |
 1 | 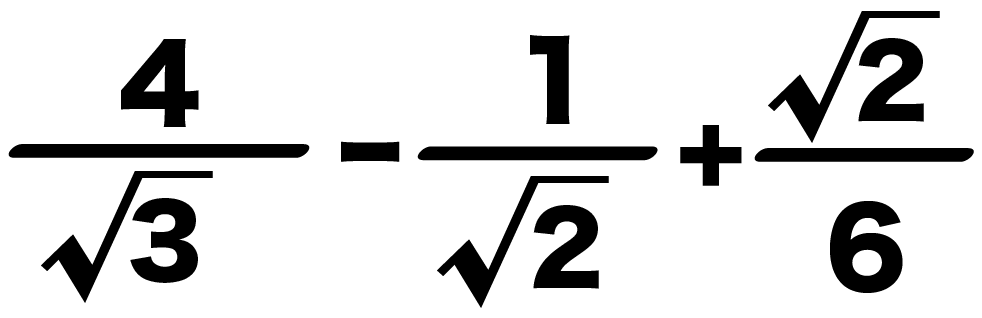 1 |  1 |
 1 |  1 |  1 |
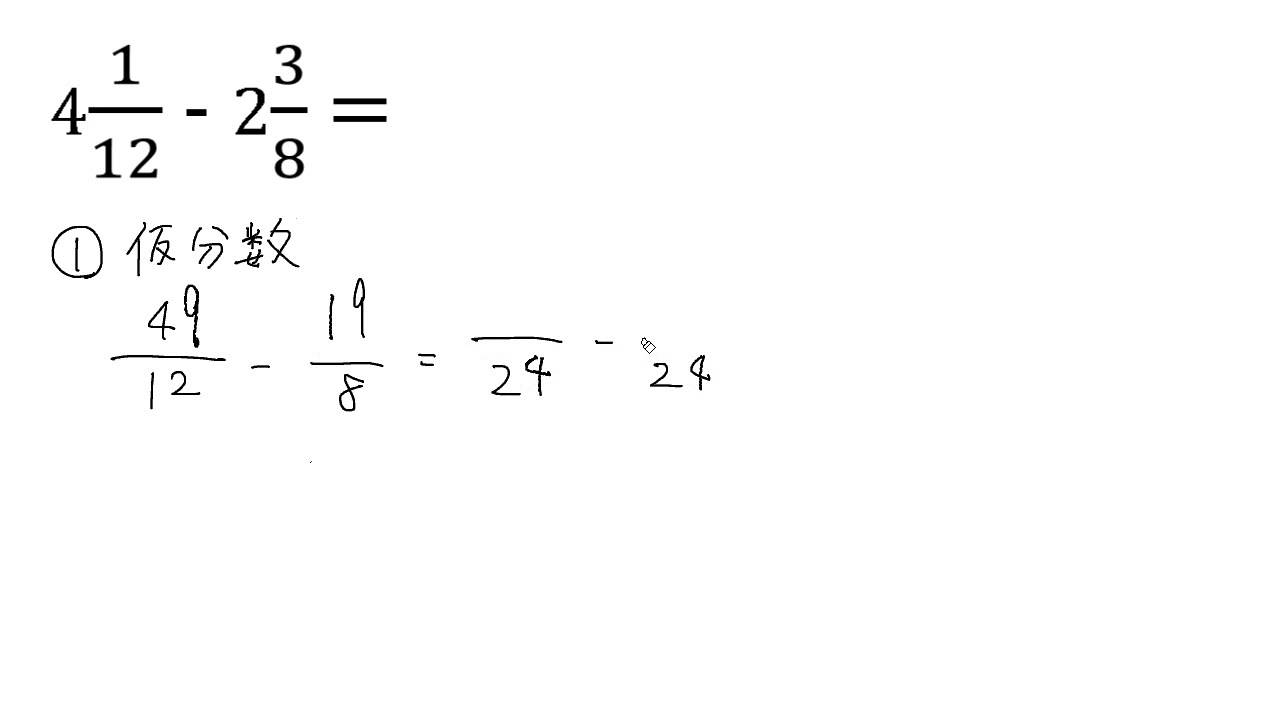 1 | 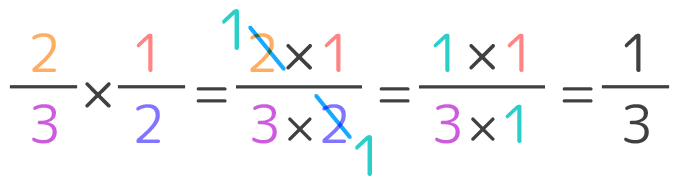 1 | 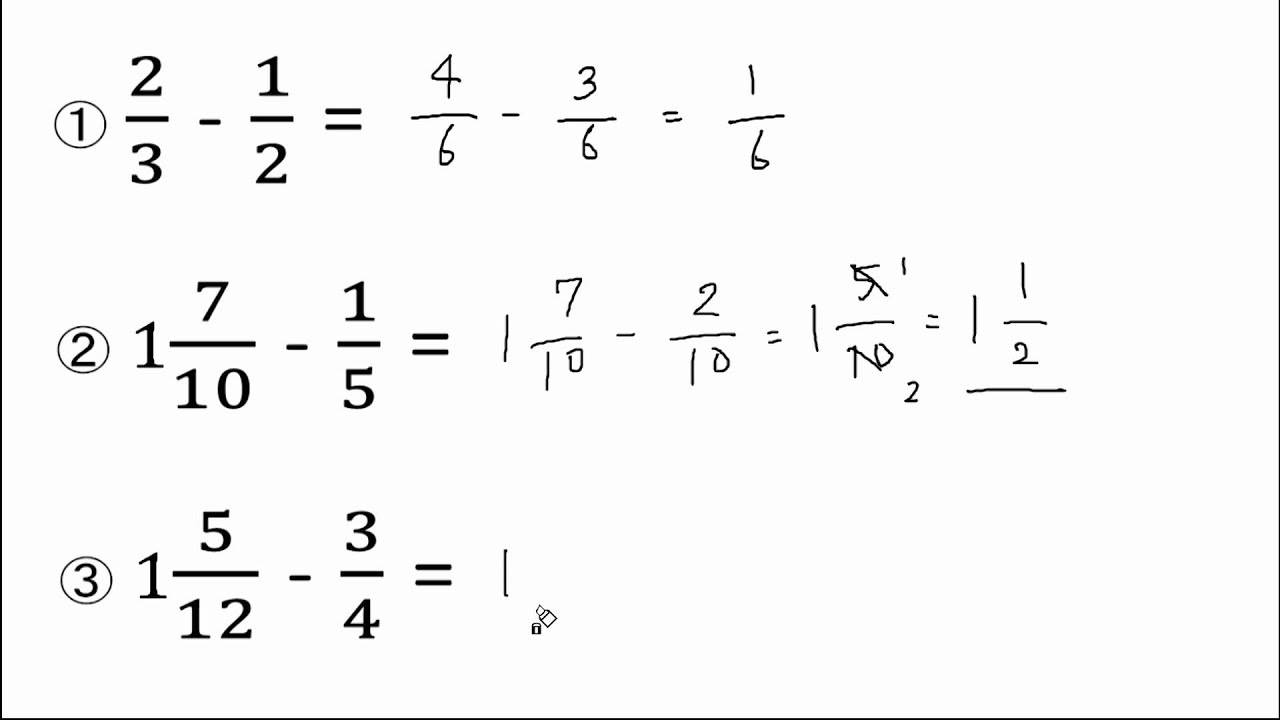 1 |
 1 | 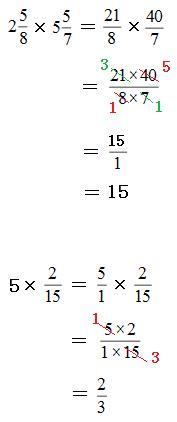1 |  1 |
 1 |  1 |  1 |
 1 | 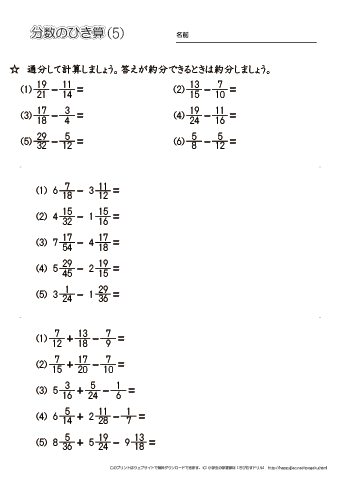 1 | 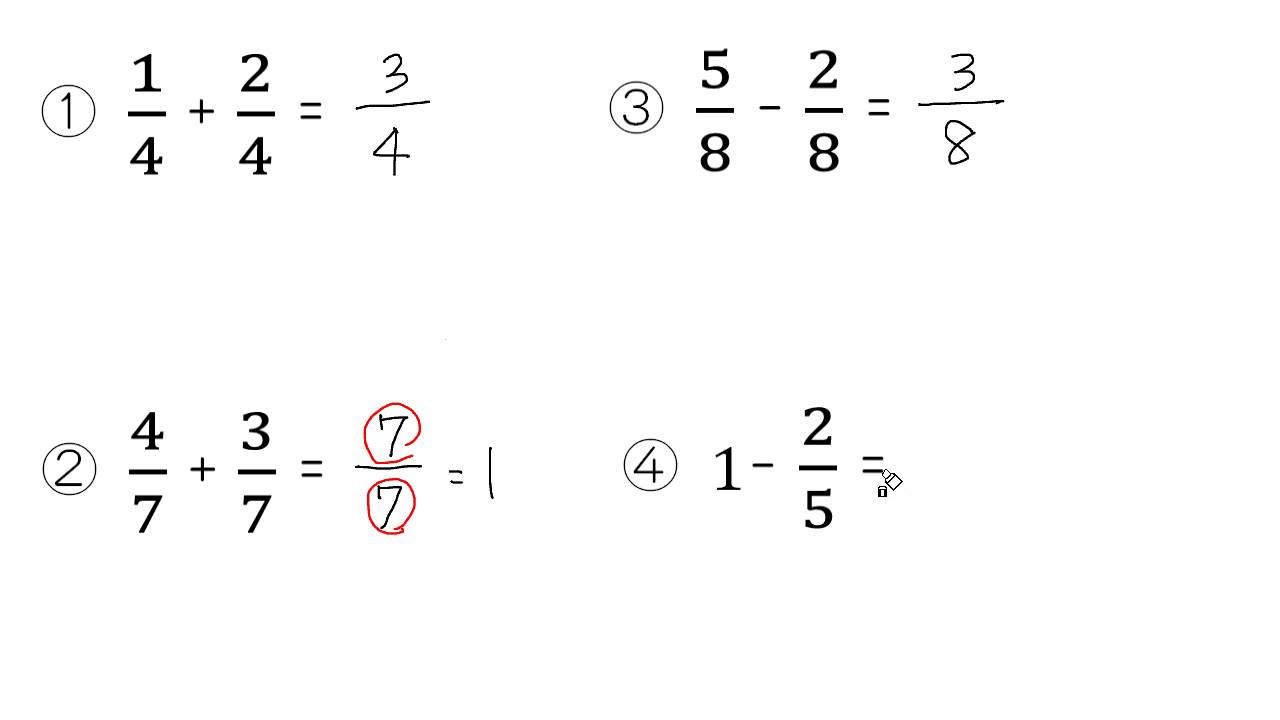 1 |
 1 |  1 |
分数式の足し算・引き算の復習 次の計算をしてみましょう。\ \frac{x^2x2}{x1} \frac{x^2x2}{x1} \ 分数式の足し算や引き算は、分母が同じになるように通分してから、分子を ですから、メール打つ時はメール打つのに集中する。 仕様書書く時は仕様書を書く。 みたいに同じ種類の処理はまとめて行うと速いですし、ミスも少なくなります。 勉強も一緒です
0 件のコメント:
コメントを投稿